 Image credit: Martinez-Minaya et al. (2023)
Image credit: Martinez-Minaya et al. (2023)
Abstract
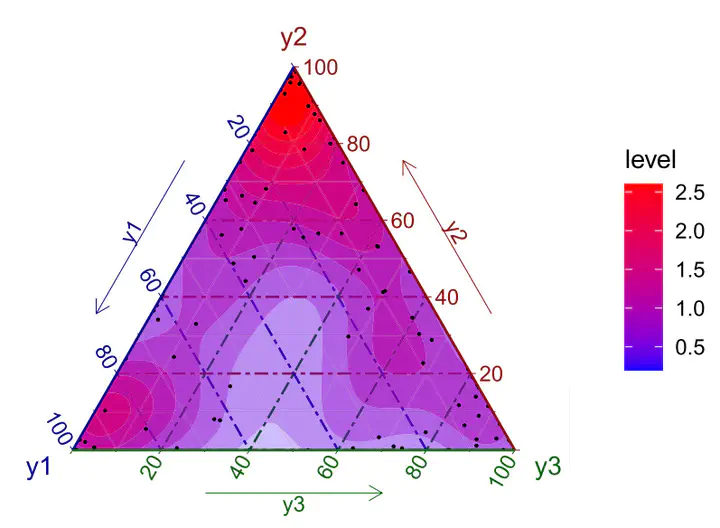
This article introduces a Laplace approximation to Bayesian inference in Dirichlet regression models, which can be used to analyze a set of variables on a simplex exhibiting skewness and heteroscedasticity, without having to transform the data. These data, which mainly consist of proportions or percentages of disjoint categories, are widely known as compositional data and are common in areas such as ecology, geology, and psychology. We provide both the theoretical foundations and a description of how Laplace approximation can be implemented in the case of Dirichlet regression. The article also introduces the package dirinla in the R-language that extends the R-INLA package, which can not deal directly with Dirichlet likelihoods. Simulation studies are presented to validate the good behavior of the proposed method, while a real data case-study is used to show how this approach can be applied.
Type
Publication
Journal of Computational and Graphical Statistics