A flexible Bayesian tool for CoDa mixed models: logistic-normal distribution with Dirichlet covariance
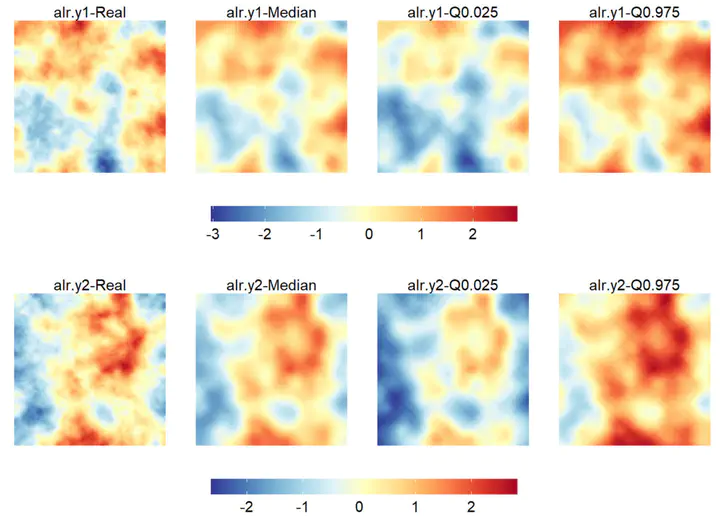 Image credit: Martinez-Minaya and Rue (2024)
Image credit: Martinez-Minaya and Rue (2024)
Abstract
Compositional Data Analysis (CoDa) has gained popularity in recent years. This type of data consists of values from disjoint categories that sum up to a constant. Both Dirichlet regression and logistic-normal regression have become popular as CoDa analysis methods. However, fitting this kind of multivariate models presents challenges, especially when structured random effects are included in the model, such as temporal or spatial effects. To overcome these challenges, we propose the logistic-normal Dirichlet Model (LNDM). We seamlessly incorporate this approach into the R-INLA package, facilitating model fitting and model prediction within the framework of Latent Gaussian Models. Moreover, we explore metrics like Deviance Information Criteria, Watanabe Akaike information criterion, and cross-validation measure conditional predictive ordinate for model selection in R-INLA for CoDa. Illustrating LNDM through two simulated examples and with an ecological case study on Arabidopsis thaliana in the Iberian Peninsula, we underscore its potential as an effective tool for managing CoDa and large CoDa databases.
Type
Publication
Statistics and Computing