A hierarchical Bayesian Beta regression approach to study the effects of geographical genetic structure and spatial autocorrelation on species distribution range shifts
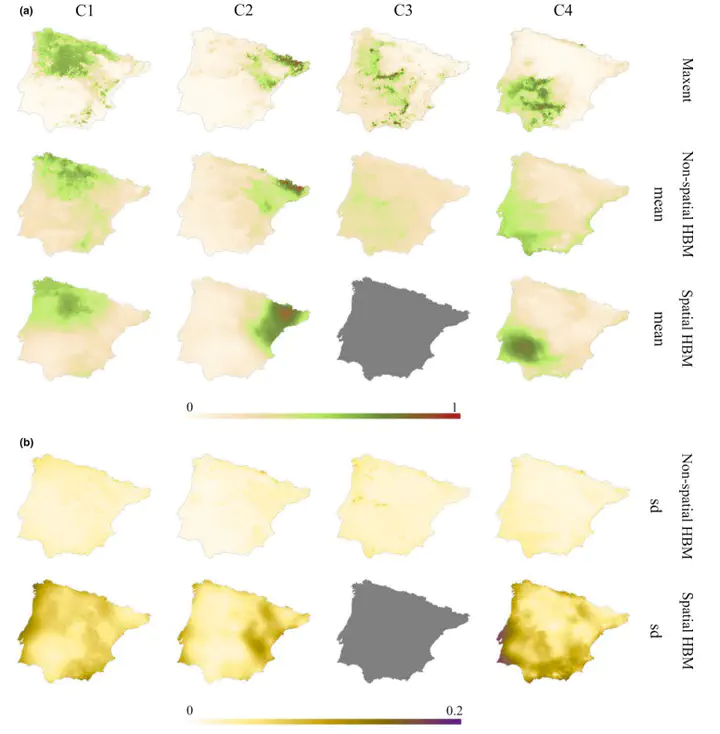 Image credit: Martinez-Minaya et al. (2019)
Image credit: Martinez-Minaya et al. (2019)
Resumen
Global climate change (GCC) may be causing distribution range shifts in many organisms worldwide. Multiple efforts are currently focused on the development of models to better predict distribution range shifts due to GCC. We addressed this issue by including intraspecific genetic structure and spatial autocorrelation (SAC) of data in distribution range models. Both factors reflect the joint effect of ecoevolutionary processes on the geographical heterogeneity of populations. We used a collection of 301 georeferenced accessions of the annual plant Arabidopsis thaliana in its Iberian Peninsula range, where the species shows strong geographical genetic structure. We developed spatial and nonspatial hierarchical Bayesian models (HBMs) to depict current and future distribution ranges for the four genetic clusters detected. We also compared the performance of HBMs with Maxent (a presence-only model). Maxent and nonspatial HBMs presented some shortcomings, such as the loss of accessions with high genetic admixture in the case of Maxent and the presence of residual SAC for both. As spatial HBMs removed residual SAC, these models showed higher accuracy than nonspatial HBMs and handled the spatial effect on model outcomes. The ease of modelling and the consistency among model outputs for each genetic cluster was conditioned by the sparseness of the populations across the distribution range. Our HBMs enrich the toolbox of software available to evaluate GCC-induced distribution range shifts by considering both genetic heterogeneity and SAC, two inherent properties of any organism that should not be overlooked.
Tipo
Publicación
Molecular ecology resources 19(4), 929 - 943